19  Multiple linear regression

19.1 Setup

First we load the dataset and have a glimpse at it.

library(tidyverse)
birth <- read_csv("datasets/birth.csv") # Remember to set the correct path
# Recoding sex as factor
birth <- birth |>  mutate(sex = as.factor(ifelse(sex == 1, "Male", "Female")))
glimpse(birth)

Rows: 230
Columns: 7
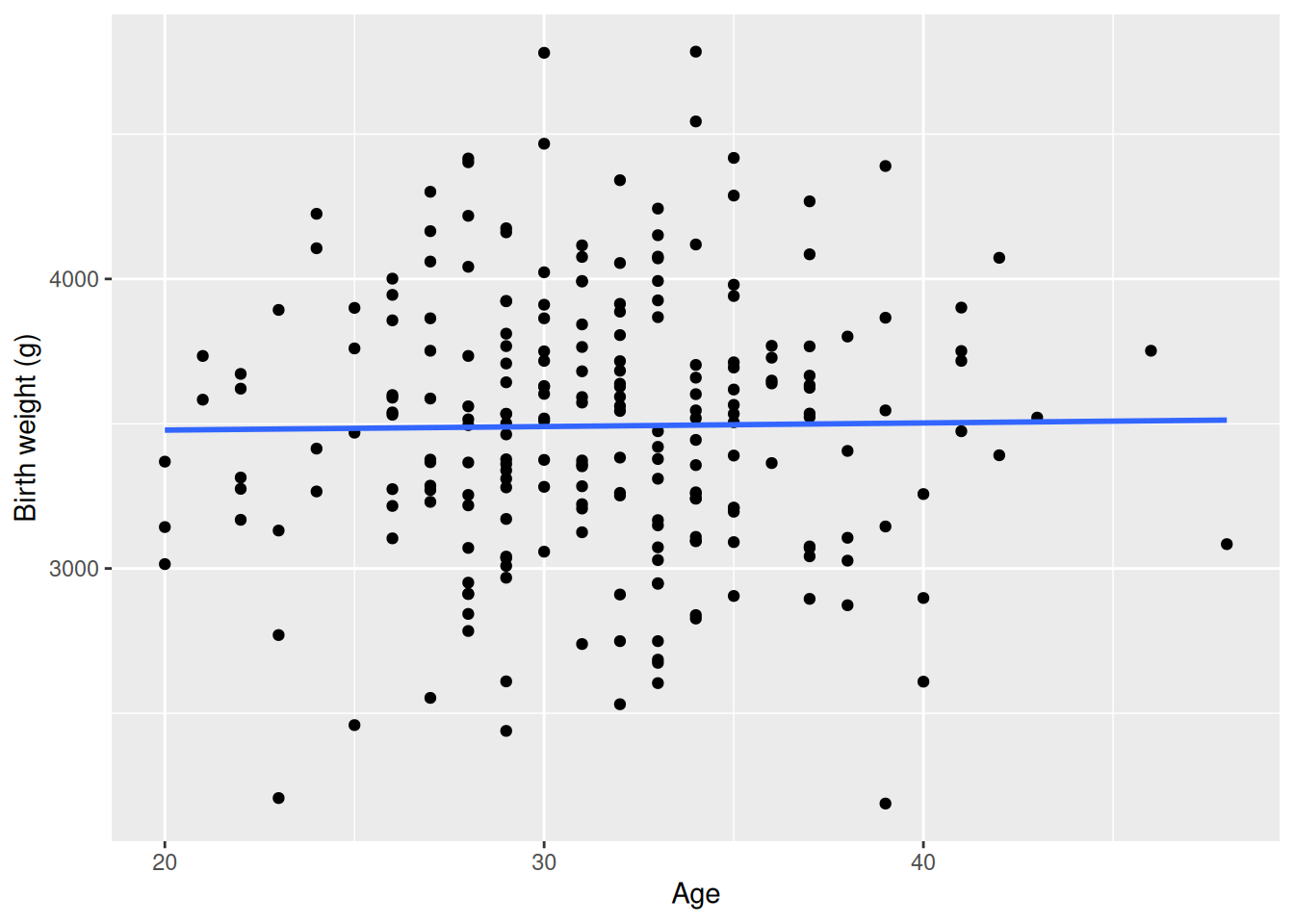
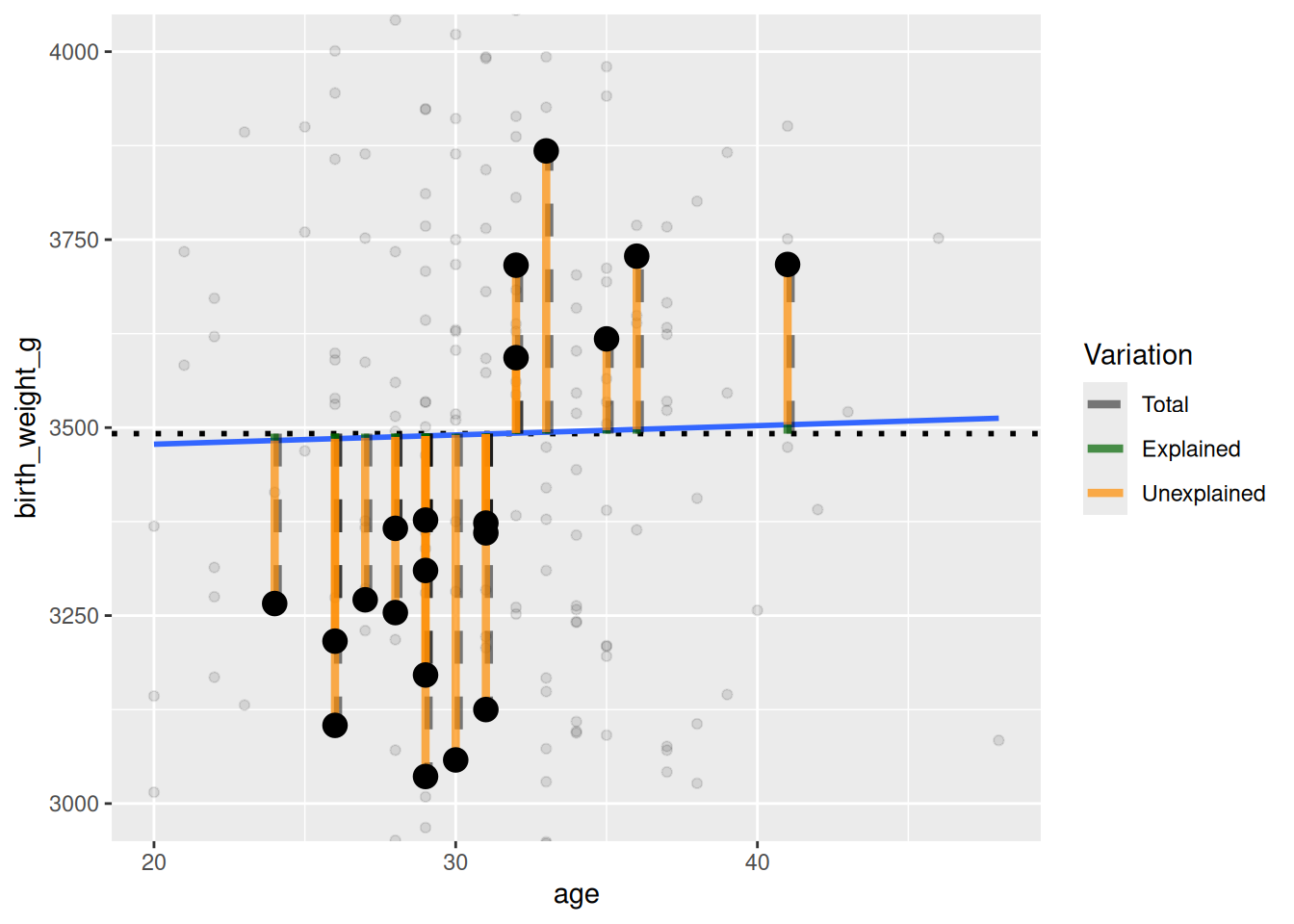
$ birth_weight_g         <dbl> 4073, 4060, 3071, 3546, 3222, 3420, 3106, 3274,…
$ pregnancy_duration_wks <dbl> 41, 40, 39, 39, 39, 41, 40, 40, 40, 41, 41, 38,…
$ sex                    <fct> Male, Female, Female, Male, Female, Male, Femal…
$ age                    <dbl> 42, 27, 37, 39, 31, 33, 38, 26, 30, 35, 29, 29,…
$ length_cm              <dbl> 176, 180, 171, 167, 158, 166, 169, 164, 167, 16…
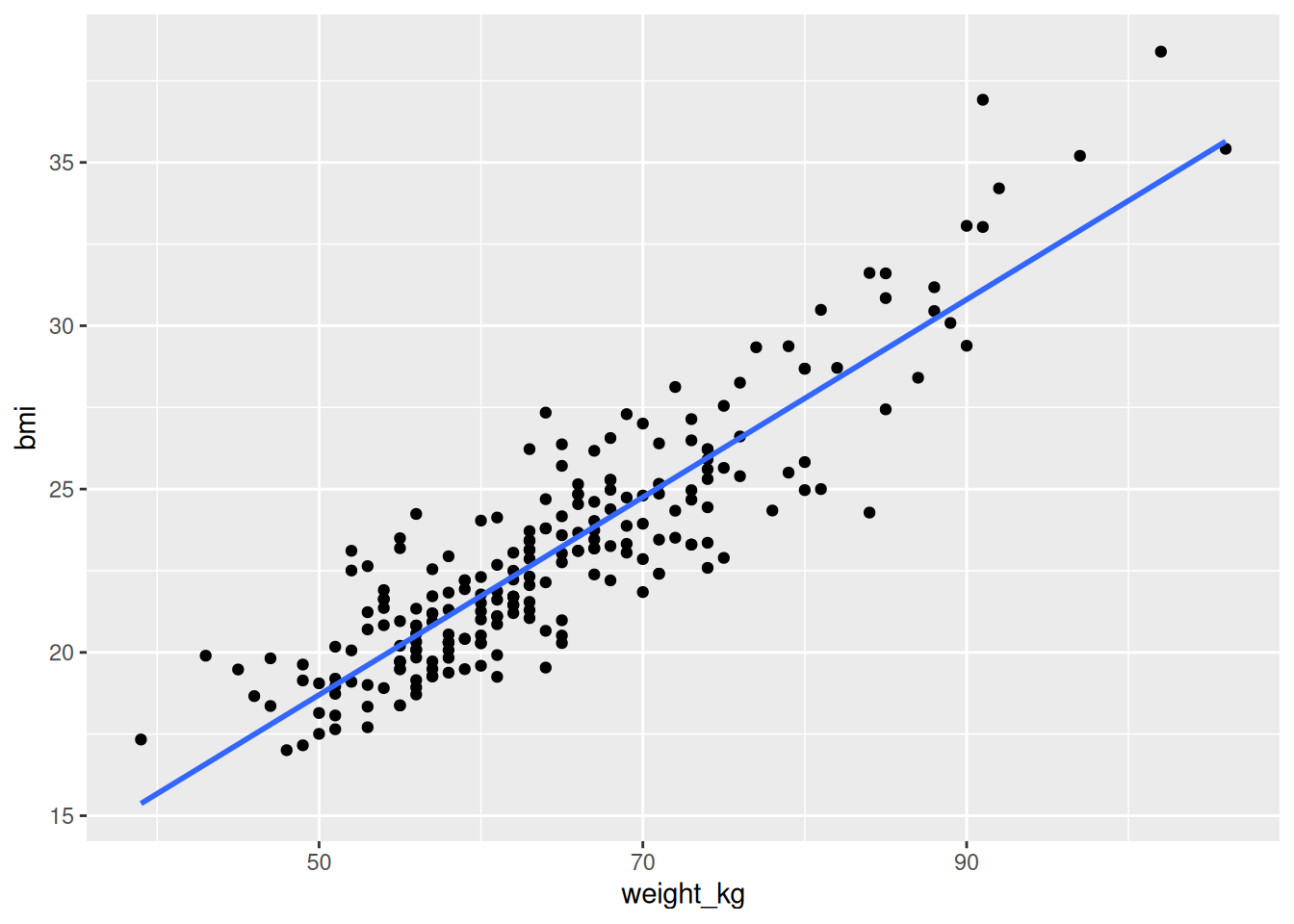
$ weight_kg              <dbl> 65, 81, 70, 80, 54, 50, 50, 65, 80, 55, 57, 63,…
$ bmi                    <dbl> 20.98399, 25.00000, 23.93899, 28.68514, 21.6311…

19.2 Birth weight dataset

19.2.1 Exercise 1

We don’t know anything else than that the sample was collected in Sweden, so our population is children born in Sweden. It would be useful to know more about where the children was born to better specify the population, and when they were born.

Information about the father, ethnicity, and health related variables such as smoking and blood pressure would be interesting.

19.2.2 Exercise 2

The null and alternative hypotheses are

\(H_0\): There is no linear relationship between the mothers age and the birth weight of the child.

\(H_a\): There is a linear relationship between the mothers age and the birth weight of the child.

We perform linear regression with age as our predictor.

model_summary <- birth |> 
  lm(formula = birth_weight_g ~ age) |> 
  summary()
model_summary$coefficients

               Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 3453.230738 201.341654 17.151099 6.616019e-43
age            1.233859   6.336775  0.194714 8.457902e-01

We see that the \(p\)-value is \(\sim0.85\), so we conclude that there is no significant linear relationship between the birth weight and the mothers age.

19.2.3 Exercise 3

We fit the three linear models separately.

# Mother length
model_summary <- birth |> 
  lm(formula = birth_weight_g ~ length_cm) |> 
  summary()
model_summary$coefficients

             Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 108.03363 767.697547 0.1407242 8.882121e-01
length_cm    20.25099   4.590836 4.4111770 1.585424e-05

# Mother weight
model_summary <- birth |> 
  lm(formula = birth_weight_g ~ weight_kg) |> 
  summary()
model_summary$coefficients

               Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 2974.057674  179.75748 16.544834 6.358329e-41
weight_kg      8.032416    2.74819  2.922803 3.818211e-03

# Mother BMI
model_summary <- birth |> 
  lm(formula = birth_weight_g ~ bmi) |> 
  summary()
model_summary$coefficients

               Estimate Std. Error   t value     Pr(>|t|)
(Intercept) 3294.148417 193.123860 17.057180 1.340283e-42
bmi            8.570779   8.260604  1.037549 3.005793e-01

We see that the \(p\)-values for length and weight are below the significance level 0.05 but not BMI.

19.3 Comparing models

19.3.1 Selecting between two simple linear regression models

The linear relationship was not significant so we would not expect age to explain much of the variation of birth_weight_g.

model_summary <- birth |> 
  lm(formula = birth_weight_g ~ age) |> 
  summary()
model_summary$r.squared

[1] 0.0001662599

In our plot we can see that the line is almost completely flat.

birth |> 
  ggplot(aes(x = age, y = birth_weight_g)) +
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE) +
  labs(
    x = "Age",
    y = "Birth weight (g)")

`geom_smooth()` using formula = 'y ~ x'

We can also look at a few selected points and look at their explained variation like in the chapter. We see that almost all variation is unexplained. Note: You were not asked to do this visualization on your own.

Code

# Limits
ylims <- c(3000, 4000)
# Predictions
model <- birth |> lm(formula = birth_weight_g ~ age)
# Subset points to show
set.seed(1337)
subset_birth <- birth |> 
  mutate(
    pred = predict(model),
    resid = resid(model)) |> 
  filter(
    (age < mean(birth$age) & birth_weight_g < pred - 100) |
    (age > mean(birth$age) & birth_weight_g > pred + 100)) |>  
  filter(birth_weight_g < 4000 & birth_weight_g > 3000) |> 
  sample_n(20)
# Calculate mean of birth weight
mean_bw <- birth |> pull(birth_weight_g) |> mean()

birth |> 
  ggplot(aes(
    x = age, 
    y = birth_weight_g)) + 
  geom_hline(
    yintercept = mean_bw,
    linetype = 3,
    linewidth = 1) +
  geom_point(alpha = 0.1) + 
  geom_smooth(method = "lm", se = FALSE) +
  geom_segment( # Total variation
    data = subset_birth,
    aes(
      x = age + 0.1,
      xend = age + 0.1,
      y =  mean_bw,
      yend = birth_weight_g,
      col = "Total"),
    linetype = 2,
    linewidth = 1.5,
    alpha = 0.5) +
    geom_segment( # Unexplained variation
    data = subset_birth,
    aes(
      x = age,
      xend = age,
      y =  pred,
      yend = birth_weight_g,
      col = "Unexplained"),
    linewidth = 1.5,
    alpha = 0.7
    ) +
  geom_segment( # Explained variation
    data = subset_birth,
    aes(
      x = age,
      xend = age,
      y =  mean_bw,
      yend = pred,
      col = "Explained"),
    linewidth = 1.5,
    alpha = 0.7
    ) +
  geom_point(data = subset_birth, size = 4) + 
  labs(
    col = "Variation") +
  scale_color_manual(
    values = c(
      "Total" = "black",
      "Explained" = "darkgreen", 
      "Unexplained" = "darkorange"),
    breaks = c(
      "Total", "Explained", "Unexplained")) +
  coord_cartesian(ylim = ylims)

19.3.2 Exercise 2

We fit a multiple linear regression model using the provided formula.

model <- birth |> lm(formula = birth_weight_g ~ weight_kg + length_cm)
model |> summary()

Call:
lm(formula = birth_weight_g ~ weight_kg + length_cm, data = birth)

Residuals:
     Min       1Q   Median       3Q      Max 
-1252.37  -286.14    11.38   271.66  1224.75 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  279.653    774.487   0.361 0.718374    
weight_kg      4.255      2.881   1.477 0.141141    
length_cm     17.582      4.923   3.572 0.000433 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 447 on 227 degrees of freedom
Multiple R-squared:  0.0874,    Adjusted R-squared:  0.07936 
F-statistic: 10.87 on 2 and 227 DF,  p-value: 3.103e-05

Including both weight_kg and length_cm increase R\(^2\) by a little, 0.0874 compared to 0.0786 when using only length_cm. It is possible that a lot of the variation explained by weight is also explained by length, as it is reasonable to believe that longer women also weigh more, on average.

19.3.3 Exercise 3

We see that our regression model is visualize as a plane in 3D space, where we can vary both weight_kg and length_cm. In general we will not visualize multiple linear regression models, and in fact any model containing more than two predictors is not possible to visualize. Understanding the visualization requires some geometrical intuition, and if you struggle to understand the visualization you can focus on interpreting the models instead, as it is more important.

Note: We are working on rendering this for the published lecture notes. You can see the visualization in the Multiple linear regression module on Canvas.

19.4 Fitting multiple linear regression models

19.4.1 Interpreting multiple linear regression

19.4.1.1 Exercise 1

We first run the code to simulate the data.

# Simulating data
set.seed(42) # Important to include this!
n_days <- 153 
n_years <- 5
month <- rep(seq(4, 8, length.out = n_days), n_years)
ice_cream_sales <- 2000 + 3000 * sin(pi * month / 14) + rnorm(length(month), 0, 200)
snake_bites <- 20 * sin(pi * month / 14) + rnorm(length(month), 0, 8)

ice_cream <- tibble(month = month, ice_cream_sales = ice_cream_sales, snake_bites = snake_bites)

We then visualize the relationship and see that there may be a linear relationship.

ice_cream |> 
  ggplot(aes(x = snake_bites, y = ice_cream_sales)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE)

`geom_smooth()` using formula = 'y ~ x'

We finally fit a regression model to see if the relationship is significant.

ice_cream |> 
  lm(formula = ice_cream_sales ~ snake_bites) |> 
  summary()

Call:
lm(formula = ice_cream_sales ~ snake_bites, data = ice_cream)

Residuals:
    Min      1Q  Median      3Q     Max 
-844.14 -179.84   17.15  193.59  709.88 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 4726.072     24.170 195.536  < 2e-16 ***
snake_bites    4.907      1.183   4.148 3.74e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 268.7 on 763 degrees of freedom
Multiple R-squared:  0.02205,   Adjusted R-squared:  0.02077 
F-statistic:  17.2 on 1 and 763 DF,  p-value: 3.735e-05

We see that the \(p\)-value is less than 0.05 and the relationship is significant with significance level 0.05.

19.4.1.2 Exercise 2

It doesn’t seem likely that snake bites increases ice cream sales, i.e. the effect doesn’t seem intuitively causal. Instead there may be another variable explaining why they correlate…

19.4.1.3 Exercise 3

We include month and fit a multiple linear regression model with hypotheses

\(H_0\): There is no linear relationship between snake bites and ice cream sales, given that month is part of the model.

\(H_a\): There is a linear relationship between snake bites and ice cream sales, given that month is part of the model.

ice_cream |> 
  lm(formula = ice_cream_sales ~ snake_bites + month) |> 
  summary()

Call:
lm(formula = ice_cream_sales ~ snake_bites + month, data = ice_cream)

Residuals:
    Min      1Q  Median      3Q     Max 
-590.93 -138.02   -0.79  142.45  746.38 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3936.8267    42.0421  93.640   <2e-16 ***
snake_bites    1.4352     0.9548   1.503    0.133    
month        142.3655     6.7454  21.106   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 213.6 on 762 degrees of freedom
Multiple R-squared:  0.3828,    Adjusted R-squared:  0.3812 
F-statistic: 236.3 on 2 and 762 DF,  p-value: < 2.2e-16

We don’t have evidence in our data that there is a linear relationship between snake bites and ice cream sales at significance level 0.05, given that the month is included in the model.

Beyond the scope of the course

If we look at the code that generated the data we can see that in fact snake_bites and ice_cream_sales are both generated based on month, but are otherwise unrelated. You do not need to understand the mathematical formula, just notice month appears on the right side of <-, indicating that the values of ice_cream_sales and snake_bites depend on month.

ice_cream_sales <- 2000 + 3000 * sin(pi * month / 14) + rnorm(length(month), 0, 200)
snake_bites <- 20 * sin(pi * month / 14) + rnorm(length(month), 0, 8)

19.5 Model selection

19.5.1 Multicollinearity

19.5.1.1 Exercise 1

Visualizing shows the linear relationship.

birth |> 
  ggplot(aes(x= weight_kg, y = bmi)) + 
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

`geom_smooth()` using formula = 'y ~ x'

Unsurprisingly, the relationship is significant and R\(^2\) is as high as 0.8.

birth |> 
  lm(formula = bmi ~ weight_kg) |> 
  summary()

Call:
lm(formula = bmi ~ weight_kg, data = birth)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.7078 -1.0939 -0.1947  0.9263  5.8122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.572167   0.653213   5.469 1.19e-07 ***
weight_kg   0.302571   0.009987  30.298  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.666 on 228 degrees of freedom
Multiple R-squared:  0.801, Adjusted R-squared:  0.8002 
F-statistic:   918 on 1 and 228 DF,  p-value: < 2.2e-16

19.5.1.2 Exercise 2

We can solve this in two ways, either by avoiding using . in our formula or by removing z from df.

Code

set.seed(42) # Setting seed for reproducibility
x <- seq(1, 100) + rnorm(100, 0, 2)
y <- 3 * x + rnorm(100, 0, 2)
z <- rep(NA, 100)

df <- data.frame(x = x, y = y, z = z)

model1 <- df |> lm(formula = y ~ x)
model1_summary <- model1 |> summary()
model1_summary$r.squared
model2 <- df |> 
  select(!z) |> 
  lm(formula = y ~ .)
model2_summary <- model2 |> summary()
model2_summary$r.squared

19.5.2 Model selection strategies

19.5.2.1 Exercise 1

When performing forward selection we start by fitting simple linear regression models for each of the potential predictors and add the variable that improves the adjusted R\(^2\) the most to our model. It is important to use adjusted R\(^2\) since adding any variable will increase R\(^2\) but adjusted R\(^2\) will penalize adding more variables to the model, balancing model fit and model complexity.

To keep the code as compact as possible, we will use the ; operator that has the same effect as a new line when extracting the adjusted R\(^2\) value from each model.

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks) |> summary() ; ms$adj.r.squared

[1] 0.2433635

ms <- birth |> lm(formula = birth_weight_g ~ sex) |> summary() ; ms$adj.r.squared

[1] 0.05762742

ms <- birth |> lm(formula = birth_weight_g ~ age) |> summary() ; ms$adj.r.squared

[1] -0.004218976

ms <- birth |> lm(formula = birth_weight_g ~ length_cm) |> summary() ; ms$adj.r.squared

[1] 0.07459224

ms <- birth |> lm(formula = birth_weight_g ~ weight_kg) |> summary() ; ms$adj.r.squared

[1] 0.03188758

ms <- birth |> lm(formula = birth_weight_g ~ bmi) |> summary() ; ms$adj.r.squared

[1] 0.0003339815

Unsurprisingly, pregnancy_duration_wks is the variable with the highest adjusted R\(^2\). It seems reasonable since even when they are born infants grow very fast. In the next step we fit multiple linear regression models with two predictors, the first one being pregnancy_duration_wks.

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + sex) |> summary() ; ms$adj.r.squared

[1] 0.2710353

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + age) |> summary() ; ms$adj.r.squared

[1] 0.2462937

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm) |> summary() ; ms$adj.r.squared

[1] 0.314511

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + weight_kg) |> summary() ; ms$adj.r.squared

[1] 0.2789052

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + bmi) |> summary() ; ms$adj.r.squared

[1] 0.2464091

length_cm is now the variable that increases adjusted R\(^2\) the most, so we include it in our model and continue by adding a third variable.

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex) |> summary() ; ms$adj.r.squared

[1] 0.3365938

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + age) |> summary() ; ms$adj.r.squared

[1] 0.3123593

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + weight_kg) |> summary() ; ms$adj.r.squared

[1] 0.3223792

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + bmi) |> summary() ; ms$adj.r.squared

[1] 0.3219845

sex is now the variable that increases adjusted R\(^2\) the most, so we include it in our model and continue with by a fourth variable.

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + age) |> summary() ; ms$adj.r.squared

[1] 0.3341412

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + weight_kg) |> summary() ; ms$adj.r.squared

[1] 0.3449951

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + bmi) |> summary() ; ms$adj.r.squared

[1] 0.3443753

weight_kg is now the variable that increases adjusted R\(^2\) the most and is also statistically significant at significance level 0.05, so we include it in our model and continue by adding a fifth variable.

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + weight_kg + age) |> summary() ; ms$adj.r.squared

[1] 0.3426022

ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + weight_kg + bmi) |> summary() ; ms$adj.r.squared

[1] 0.3435731

Adding either age or bmi decreased our adjusted R\(^2\) and we have reached our stopping criteria. Using forward selection we found the same model as when we looked at multicollinearity and removed bmi based on domain knowledge.

# Forward selection (fs) model
model_fs <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + weight_kg)
model_fs |> summary()

Call:
lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + 
    sex + weight_kg, data = birth)

Residuals:
     Min       1Q   Median       3Q      Max 
-1000.23  -249.24    -6.36   249.70  1102.63 

Coefficients:
                        Estimate Std. Error t value Pr(>|t|)    
(Intercept)            -6504.850   1026.365  -6.338 1.26e-09 ***
pregnancy_duration_wks   175.099     20.167   8.683 7.97e-16 ***
length_cm                 15.842      4.163   3.806 0.000182 ***
sexMale                  149.730     50.465   2.967 0.003332 ** 
weight_kg                  4.800      2.431   1.975 0.049545 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 377 on 225 degrees of freedom
Multiple R-squared:  0.3564,    Adjusted R-squared:  0.345 
F-statistic: 31.15 on 4 and 225 DF,  p-value: < 2.2e-16

19.5.2.2 Exercise 2

We can use our results from the previous exercise to see if mixed selection would have given us a different model. After each forward step we check the \(p\)-values. If any variable is not significant we can conclude that mixed selection would have given a different result.

# First forward step
ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks) |> summary() ; ms$coefficients

                        Estimate Std. Error   t value     Pr(>|t|)
(Intercept)            -3867.089  852.13015 -4.538144 9.183294e-06
pregnancy_duration_wks   185.083   21.42084  8.640327 9.938670e-16

# Second forward step
ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm) |> summary() ; ms$coefficients

                         Estimate  Std. Error   t value     Pr(>|t|)
(Intercept)            -7075.6886 1036.945658 -6.823587 7.987029e-11
pregnancy_duration_wks   183.3006   20.392024  8.988839 9.983322e-17
length_cm                 19.6258    3.951779  4.966319 1.341270e-06

# Third forward step
ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex) |> summary() ; ms$coefficients

                          Estimate  Std. Error   t value     Pr(>|t|)
(Intercept)            -6670.10127 1029.486946 -6.479054 5.704978e-10
pregnancy_duration_wks   174.36396   20.292184  8.592666 1.411882e-15
length_cm                 18.86122    3.896383  4.840700 2.397739e-06
sexMale                  148.54634   50.783535  2.925089 3.794448e-03

# Fourth forward step
ms <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + length_cm + sex + weight_kg) |> summary() ; ms$coefficients

                           Estimate  Std. Error   t value     Pr(>|t|)
(Intercept)            -6504.849584 1026.365436 -6.337752 1.257868e-09
pregnancy_duration_wks   175.098880   20.166721  8.682566 7.969632e-16
length_cm                 15.841621    4.162720  3.805594 1.823702e-04
sexMale                  149.730071   50.464514  2.967037 3.331594e-03
weight_kg                  4.799832    2.430882  1.974523 4.954531e-02

No variable became not significant after each forward step. We conclude that mixed selection would have given us the same model as forward selection in this case.

19.5.2.3 Exercise 3

We first remember the variables in the penguins dataset.

library(palmerpenguins)
glimpse(penguins)

Rows: 344
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <fct> male, female, female, NA, female, male, female, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

We then start by fitting a regression model using all potential predictors.

penguins |> lm(formula = body_mass_g ~ .) |> summary()

Call:
lm(formula = body_mass_g ~ ., data = penguins)

Residuals:
    Min      1Q  Median      3Q     Max 
-809.70 -180.87   -6.25  176.76  864.22 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       84087.945  41912.019   2.006  0.04566 *  
speciesChinstrap   -282.539     88.790  -3.182  0.00160 ** 
speciesGentoo       890.958    144.563   6.163 2.12e-09 ***
islandDream         -21.180     58.390  -0.363  0.71704    
islandTorgersen     -58.777     60.852  -0.966  0.33482    
bill_length_mm       18.964      7.112   2.667  0.00805 ** 
bill_depth_mm        60.798     20.002   3.040  0.00256 ** 
flipper_length_mm    18.504      3.128   5.915 8.46e-09 ***
sexmale             378.977     48.074   7.883 4.95e-14 ***
year                -42.785     20.949  -2.042  0.04194 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 286.5 on 323 degrees of freedom
  (11 observations deleted due to missingness)
Multiple R-squared:  0.8768,    Adjusted R-squared:  0.8734 
F-statistic: 255.4 on 9 and 323 DF,  p-value: < 2.2e-16

We see that both coefficients relating to island are not significant, so we remove island from our model.

penguins |> lm(formula = body_mass_g ~ . - island) |> summary() 

Call:
lm(formula = body_mass_g ~ . - island, data = penguins)

Residuals:
    Min      1Q  Median      3Q     Max 
-809.15 -179.43   -3.42  183.60  866.03 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       80838.770  41677.817   1.940 0.053292 .  
speciesChinstrap   -274.496     81.558  -3.366 0.000855 ***
speciesGentoo       929.275    136.036   6.831 4.16e-11 ***
bill_length_mm       18.997      7.086   2.681 0.007718 ** 
bill_depth_mm        60.749     19.926   3.049 0.002487 ** 
flipper_length_mm    18.064      3.088   5.849 1.20e-08 ***
sexmale             382.168     47.797   7.996 2.28e-14 ***
year                -41.139     20.832  -1.975 0.049131 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 286.1 on 325 degrees of freedom
  (11 observations deleted due to missingness)
Multiple R-squared:  0.8764,    Adjusted R-squared:  0.8738 
F-statistic: 329.3 on 7 and 325 DF,  p-value: < 2.2e-16

19.6 Prediction

19.6.1 Exercise 1

We first note that model_fs and model_de are the same models.

model_de <- birth |> 
  lm(formula = birth_weight_g ~ . - bmi - age)
prediction <- predict(
  model_de, 
  data.frame(
    sex = "Female", 
    pregnancy_duration_wks = 40, 
    weight_kg = 68, 
    bmi = 24, 
    length_cm = 170, 
    age = 0))
prediction

      1 
3518.57 

We see that the prediction differs slightly compared to model_bs that predicted \(\sim 3492\) grams compared to model_des 3518 g. Would you say that the difference is relevant?

19.6.2 Exercise 2

# Prediction interval by backward selection model
model_bs <- birth |> lm(formula = birth_weight_g ~ pregnancy_duration_wks + sex + weight_kg + bmi)
predict(
  model_bs, 
  data.frame(
    sex = "Female", 
    pregnancy_duration_wks = 40, 
    weight_kg = 68, 
    bmi = 24),
  interval = "prediction")

       fit     lwr      upr
1 3491.656 2745.76 4237.552

# Prediction interval by backward selection model
model_de <- birth |> 
  lm(formula = birth_weight_g ~ . - bmi - age)
predict(
  model_de, 
  data.frame(
    sex = "Female", 
    pregnancy_duration_wks = 40, 
    weight_kg = 68, 
    bmi = 24, 
    length_cm = 170, 
    age = 0),
  interval = "prediction")

      fit      lwr      upr
1 3518.57 2771.581 4265.558

The predictions overlap quite a lot. In this case the models seem very similar and it shouldn’t matter much which one we use, at least for this particular prediction.