8  Logistic regression

When our outcome (dependent) is categorical, linear regression is not the best option because there is no order and/or distance between the values the variable can take on, see Section 2.2.2. Modeling the relationship between continuous (or categorical) variables and a categorical variable is sometimes called classification, because we want to classify an observation in a certain class, in a certain category. This could be any qualitative variable, such as eye color or customer satisfaction. For binary variables, one of the most common methods to achieve this is logistic regression. This allows us to ask yes and no questions.

For a more technical/mathematical introduction to logistic regression, please consult the chapter on logistic regression in An Introduction to Statistical Learning.

8.1 The Pima Indians dataset

To demonstrate logistic regression we will use the PimaIndiansDiabetes2 dataset from the mlbench package. The dataset is commonly used to test classification algorithms, predicting the onset of diabetes. The subjects consists of women aged 21 or older of the Pima Indian population. Measurements of the potential predictors were made every other year, but only one measurement per person is included in our dataset. A subject was classified as diabetic, according to WHO’s criteria, if a subject had a Glucose Tolerance Test (GTT) show more than 200 mg/dl 2 hours after ingesting 75 g of carbohydrate solution within five years of the included measurement. To better understand the case selection, look at section 2.3 in the original paper. Below is a table of the potential predictors and the outcome, diabetes, and their descriptions from running ?PimaIndiansDiabetes2.

Variable	Description
pregnant	Number of times pregnant
glucose	Plasma glucose concentration (glucose tolerance test)
pressure	Diastolic blood pressure (mm Hg)
triceps	Triceps skin fold thickness (mm)
insulin	2-Hour serum insulin (mu U/ml)
mass	Body mass index (weight in kg/(height in m)^2)
pedigree	Diabetes pedigree function
age	Age (years)
diabetes	Class variable, pos/neg

We can see that the information doesn’t tell us about how diabetes was classified, risking confusion as glucose represents a GTT at an earlier time than when diabetes was classified. If it would have been the at the same time glucose would have been a perfect predictor for diabetes, as glucose \(> 200\) would imply diabetic and glucose \(< 200\) not diabetic. This highlights the importance of understanding the dataset and the context, as presenting these results to a diabetes researcher without this information would be embarrassing.

Now when we know how the dataset was created, let’s take a glimpse at it.

library(tidyverse)
#install.packages("mlbench") # Install to get PimaIndiansDiabetes2 dataset
library(mlbench)
data("PimaIndiansDiabetes2") # Using 2 because it is a corrected version.
glimpse(PimaIndiansDiabetes2)

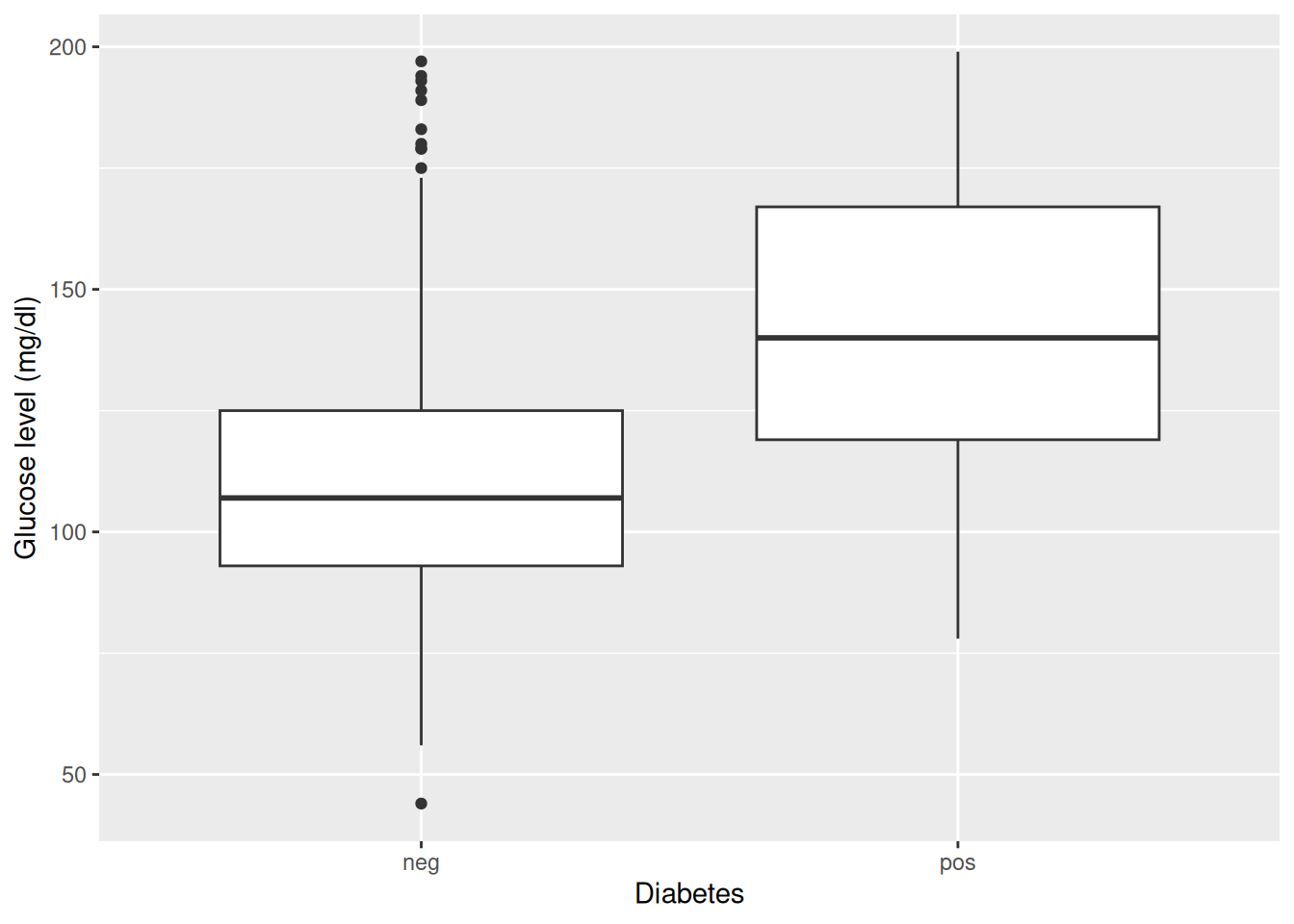
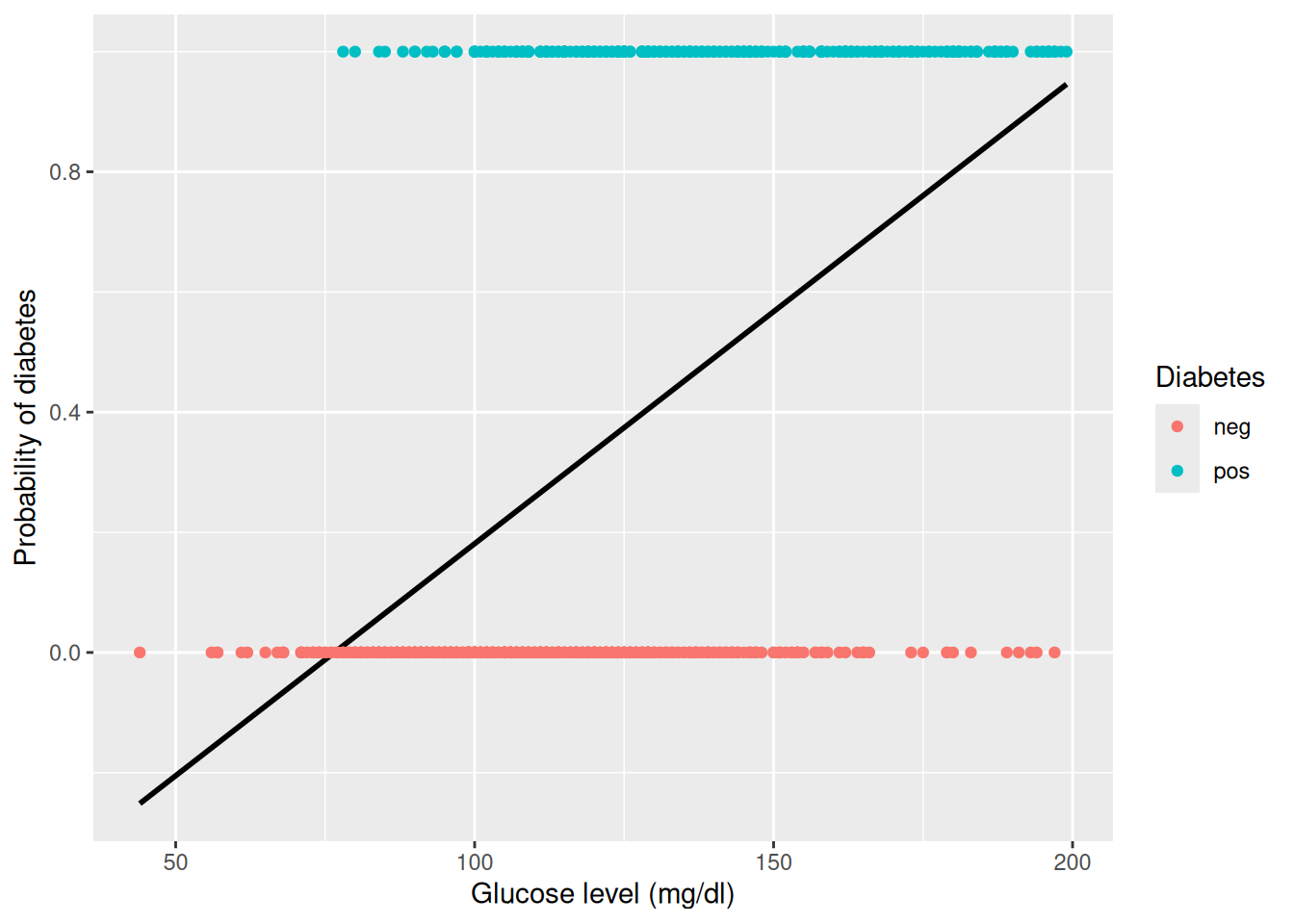
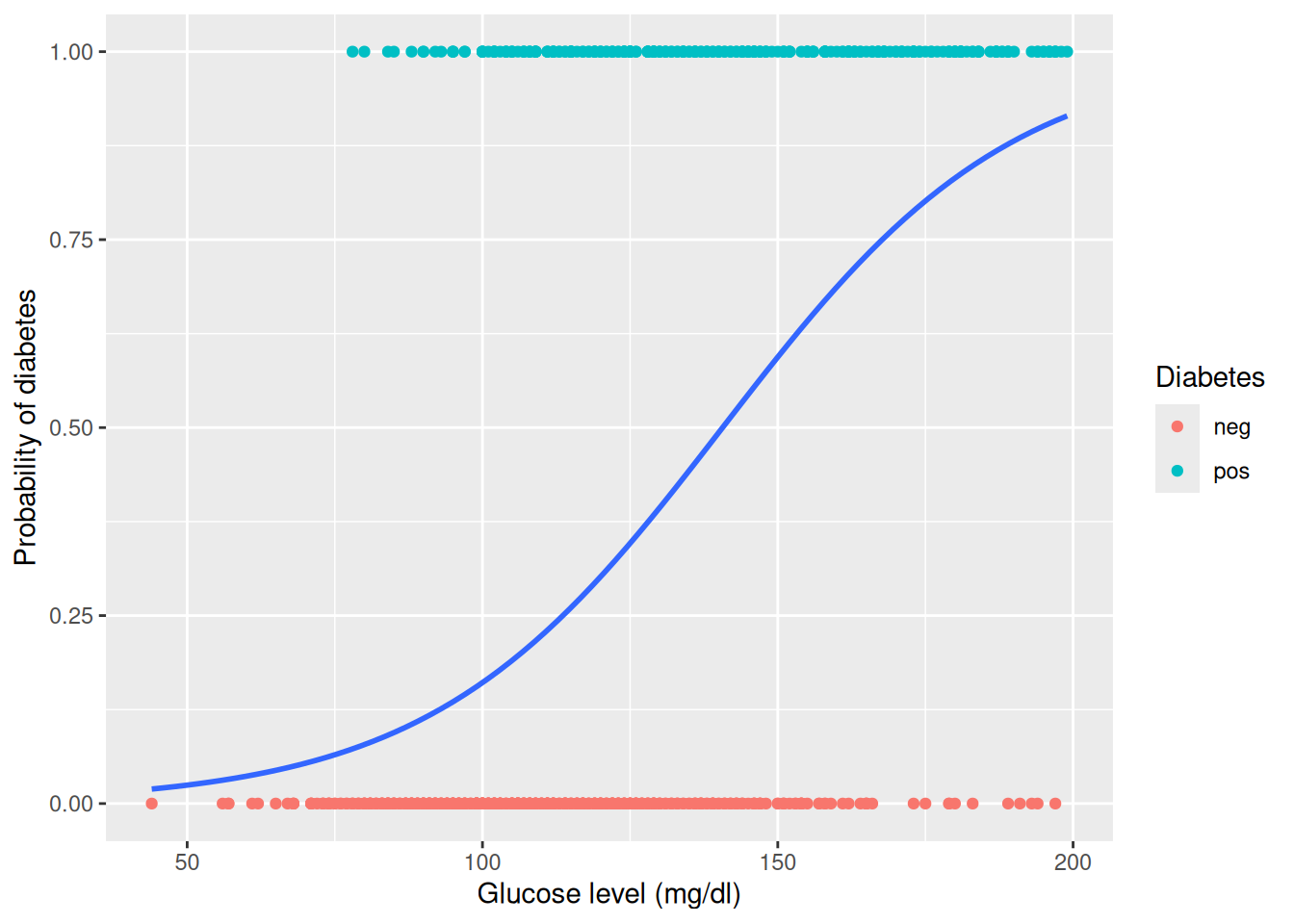
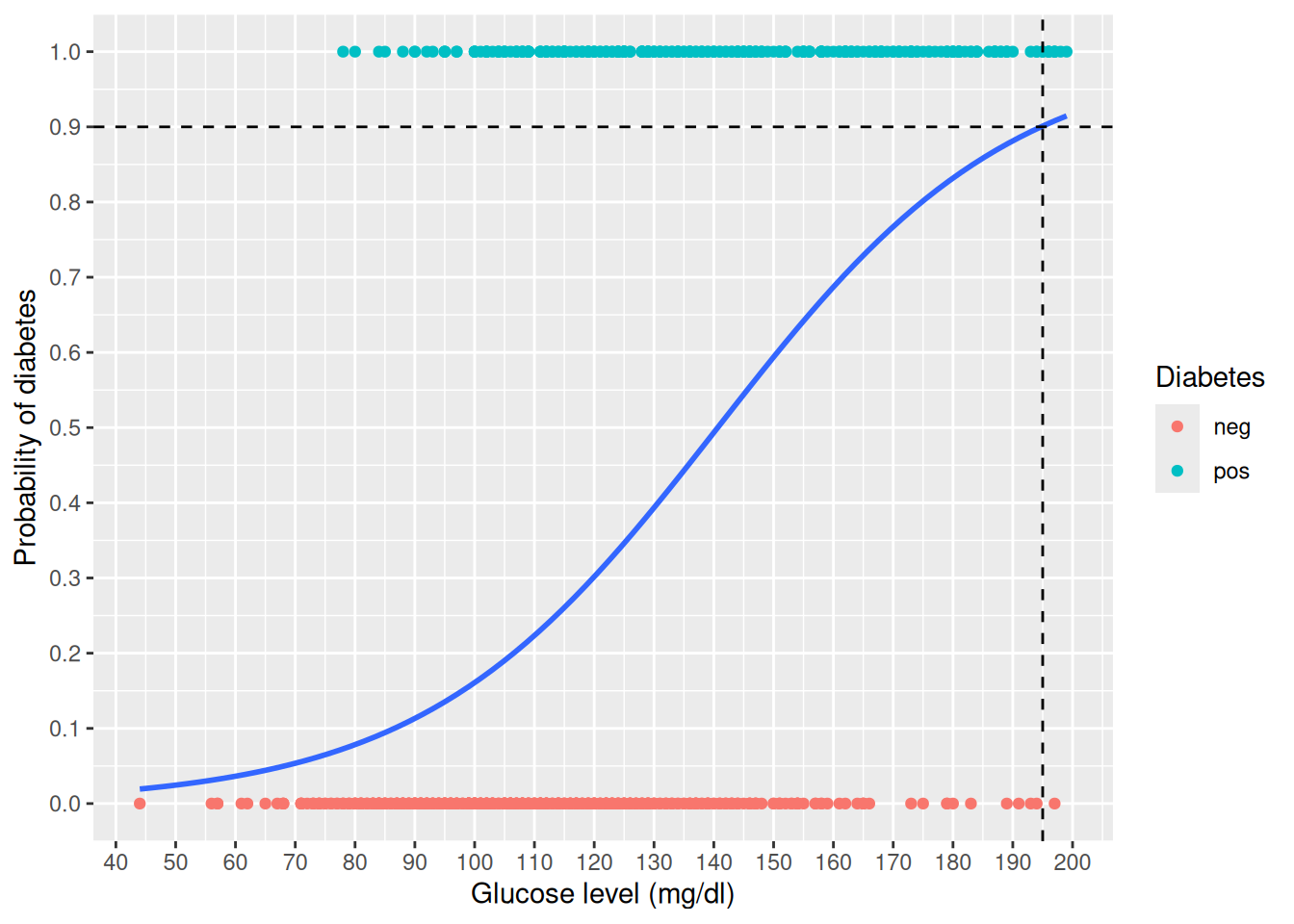
Rows: 768
Columns: 9
$ pregnant <dbl> 6, 1, 8, 1, 0, 5, 3, 10, 2, 8, 4, 10, 10, 1, 5, 7, 0, 7, 1, 1…
$ glucose  <dbl> 148, 85, 183, 89, 137, 116, 78, 115, 197, 125, 110, 168, 139,…
$ pressure <dbl> 72, 66, 64, 66, 40, 74, 50, NA, 70, 96, 92, 74, 80, 60, 72, N…
$ triceps  <dbl> 35, 29, NA, 23, 35, NA, 32, NA, 45, NA, NA, NA, NA, 23, 19, N…
$ insulin  <dbl> NA, NA, NA, 94, 168, NA, 88, NA, 543, NA, NA, NA, NA, 846, 17…
$ mass     <dbl> 33.6, 26.6, 23.3, 28.1, 43.1, 25.6, 31.0, 35.3, 30.5, NA, 37.…
$ pedigree <dbl> 0.627, 0.351, 0.672, 0.167, 2.288, 0.201, 0.248, 0.134, 0.158…
$ age      <dbl> 50, 31, 32, 21, 33, 30, 26, 29, 53, 54, 30, 34, 57, 59, 51, 3…
$ diabetes <fct> pos, neg, pos, neg, pos, neg, pos, neg, pos, pos, neg, pos, n…

We see that we have some missing values and that all potential predictors are numeric, while our outcome is binary. Knowing that a GTT of over 200 is classified as diabetic, we can start by if glucose is a good predictor for diabetes. It seems reasonable, as a person developing diabetes may already have higher glucose levels. We can visualize the relationship using boxplots to get an idea of the distribution of glucose levels in the diabetic and non-diabetic groups.

PimaIndiansDiabetes2 |>
  ggplot(aes(x = diabetes, y = glucose)) + 
  geom_boxplot() +
  labs(
    x = "Diabetes",
    y = "Glucose level (mg/dl)")

We see that the distribution of glucose level is shifted more towards higher values of the pre-diabetic women compared to the women not diagnosed with diabetes at a later stage. This indicates that glucose may be have a relationship with the onset of diabetes, which may not be surprising, but is the relationship significant? Do we expect it to hold in the population? Let’s try to model the probability of having diabetes for a given glucose level using a linear model.

8.1.1 Exercises

1. What is the population that we our sample, dataset, is drawn from?
2. Visualize the relationship between pressure, diastolic blood pressure, and diabetes. Do you suspect that pressure may be correlated with diabetes? In the next chapter we will investigate this in more detail.

8.2 Using linear regression

We may try to mutate diabetes to a numerical variable, where having diabetes is indicated by 1 and not having diabetes as 0, and use linear regression to study the effect of glucose level on the onset of diabetes.

PimaIndiansDiabetes2_numeric <- PimaIndiansDiabetes2 |>
  mutate(diabetes_num = ifelse(diabetes == "pos", 1, 0))
PimaIndiansDiabetes2_numeric |>  
  lm(formula = diabetes_num ~ glucose) |> 
  summary()

Call:
lm(formula = diabetes_num ~ glucose, data = PimaIndiansDiabetes2_numeric)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.9304 -0.2970 -0.1193  0.3322  0.9888 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.591346   0.061721  -9.581   <2e-16 ***
glucose      0.007724   0.000492  15.701   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4147 on 761 degrees of freedom
  (5 observations deleted due to missingness)
Multiple R-squared:  0.2447,    Adjusted R-squared:  0.2437 
F-statistic: 246.5 on 1 and 761 DF,  p-value: < 2.2e-16

We see that the relationship is positive and significant, but what does this actually mean? Let’s interpret the coefficient in the model. The coefficient for glucose tells us that diabetes increase with \(\sim0.007\) when glucose increases by one, but what does this mean? Diabetes is either 0 or 1, it cannot even be 0.007, so how can it increase by 0.007? What we want to model is rather the probability of diabetes to be 1 given a certain glucose level. We can visualize our linear model to see if we maybe can do that.

PimaIndiansDiabetes2_numeric |>
  ggplot(aes(x = glucose, y = diabetes_num)) +
  geom_smooth(method = "lm", se = F, col = "black") +
  geom_point(aes(col = diabetes)) +
  labs(
   x = "Glucose level (mg/dl)",
   y = "Probability of diabetes",
   col = "Diabetes")

`geom_smooth()` using formula = 'y ~ x'

Warning: Removed 5 rows containing non-finite outside the scale range
(`stat_smooth()`).

Warning: Removed 5 rows containing missing values or values outside the scale range
(`geom_point()`).

Some glucose levels seem to give a negative probability for having diabetes, which is not possible, so the interpretation of the model as assigning a probability of diabetes to a given glucose level doesn’t work either. Linear regression is not suitable for either categorical outcomes or for estimating probabilities. Instead we should use logistic regression.

8.2.1 Exercises

1. Linear regression, as you know, is useful to investigate the relationship between two continuous variables. Perform a linear regression pressure ~ mass, where mass is body mass index (BMI), and draw a conclusion based on the \(p\)-value if there is a linear relationship between the variables. State the null and alternative hypotheses.
2. Formulate the hypotheses for the test in the linear regression. Do they make sense?

8.3 Using logistic regression

Unlike linear regression, logistic regression models the probability of having diabetes for a given glucose level. It models the relationships between the explanatory variables and the outcome through the logistic function. In this course we will not go into details of the function itself, but we can visualize it

Technically logistic regression models the log-odds, but we can always transform the log-odds to probabilities.

PimaIndiansDiabetes2 |>
  mutate(diabetes_num = ifelse(diabetes == "pos", 1, 0)) |> # Necessary for the geom_smooth
  ggplot(aes(x = glucose, y = diabetes_num)) +
  geom_smooth(method = "glm", method.args = list(family = "binomial"), se = FALSE) +
  geom_point(aes(col = diabetes)) +
  labs(
   x = "Glucose level (mg/dl)",
   y = "Probability of diabetes",
   col = "Diabetes")

Using logistic regression, all probabilities fall nicely within 0 and 1, and we can interpret the relationship in terms of probabilities. In this course we will only be interested in two things from the logistic regression: The sign of the regression coefficient coefficient, i.e. if it is positive or negative, and if it is statistically significant (\(p < 0.05\)). A positive coefficient means that it increases the probability of having diabetes, and vice versa for a negative coefficient. To create our logistic regression model, we use the glm function. GLM stands for “Generalized Linear Model”, and it can model more relationships than logistic, but it is the only relationship we will work with in this course. To select the logistic regression we must use the argument family = "binomial". before performing the regression we will state our hypotheses:

\(H_0\): There is no relationship between glucose level and being diagnosed with diabetes within five years.

\(H_a\): There is a relationship between glucose level and being diagnosed with diabetes within five years.

Now we are ready to fit our logistic model.

model <- glm(diabetes ~ glucose, data = PimaIndiansDiabetes2, family = "binomial")
summary(model)

Call:
glm(formula = diabetes ~ glucose, family = "binomial", data = PimaIndiansDiabetes2)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -5.715088   0.438100  -13.04   <2e-16 ***
glucose      0.040634   0.003382   12.01   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 986.70  on 762  degrees of freedom
Residual deviance: 786.56  on 761  degrees of freedom
  (5 observations deleted due to missingness)
AIC: 790.56

Number of Fisher Scoring iterations: 4

Under “Coefficients” we find “glucose” on row three, and the estimate of the coefficient under “estimate”. We can see that it is a positive coefficient, so having a higher glucose level increases the probability of having diabetes, again as expected. We can also find the \(p\)-value in the fourth column, “Pr(>|z|)”. We see that we have a positive relationship between glucose level and the later onset of diabetes that is statistically significant. We can conclude that having a higher glucose level increases the risk of the onset of diabetes in the population of women in the Pima Indians tribe, at significance level 0.05.

8.3.1 Exercises

1. Since glucose level is used to diagnose diabetes this analysis may not be very insightful. Instead it would be interesting to find other variables that are useful for predicting diabetes. Fit logistic regressions for (a) pressure and (b) mass and analyze the results. Remember to formulate the hypotheses. In the next chapter we will continue to study these variables and their relationship with diabetes using multiple logistic regression.

8.4 Prediction

Just as with linear regression we can use our logistic model to predict the probability of having diabetes given a glucose level. Again we use the predict function with the parameter type = "response" to get the output in predicted probabilities. We can try to predict the probability of having diabetes if the glucose level is 150 mg/dl.

predict(model, data.frame(glucose = 150), type = "response")

        1 
0.5938624 

According to our model, the probability of having diabetes of a woman in the Pima Indian tribe with glucose level 150 mg/dl is 0.59.

Now we have studied the relationship between one continuous variable and the outcome. Just as with linear regression before, we can study the relationship between multiple predictors and diabetes using multiple logistic regression, which is the topic of the next chapter.

8.4.1 Exercises

1. Use your previously fitted models of diabetes ~ pressure and diabetes ~ mass to predict probabilities of getting diabetes given pressure = 90 and mass = 25.
2. Based on the following plot, what glucose level would generate a prediction of above 0.9 probability of diabetes? Verify using predict.

Code

PimaIndiansDiabetes2 |>
  mutate(diabetes_num = ifelse(diabetes == "pos", 1, 0)) |>
  ggplot(aes(x = glucose, y = diabetes_num)) +
  geom_smooth(method = "glm", method.args = list(family = "binomial"), se = FALSE) +
  geom_point(aes(col = diabetes)) +
  geom_hline(
    yintercept = 0.9,
    col = "black",
    linetype = 2) +
  geom_vline(
    xintercept = 195,
    col = "black",
    linetype = 2) +
  labs(
   x = "Glucose level (mg/dl)",
   y = "Probability of diabetes",
   col = "Diabetes") +
  scale_x_continuous(breaks = seq(40, 200, by = 10)) +
  scale_y_continuous(breaks = seq(0, 1, by = 0.1))

3. Predict the probability of the onset of diabetes given glucose = 200, i.e. the threshold for being diagnosed with diabetes. Does your prediction make sense? Is the model trained for this?